Casos de Congruência de Triângulos. Exercícios resolvidos.

Casos de Congruência de Triângulos

Casos de congruência de triângulos. Triângulos congruentes.

1. Determine se os seguintes triângulos são congruentes. Se forem congruentes diga qual caso de congruência é (preste atenção à propriedade correspondente) LLL, LAL, ALA, LAA. Se não houver congruência diga por que razão não são congruentes.

Resposta:

O triângulo ABD é congruente ao triângulo DBC pelo caso Lado Ângulo Lado (LAL).

Temos que o lado AB é congruente ao lado BC e o lado BD é lado comum aos triângulos ABD e DBC. Além disso, o ângulo B é congruente em ABD e DBC, logo os triângulos ABD e DBC são congruentes pelo caso Lado Ângulo Lado (LAL).   

Resposta:

Os triângulos não são congruentes, pois há falta de informações. Temos apenas dados de dois lados onde o lado EF é congruente ao lado HJ e o lado FG é congruente ao lado JK, e não há uma terceira informação para concluir se são congruentes.

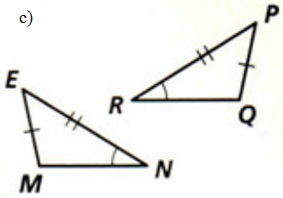
Temos que o lado EM é congruente ao lado PQ. O lado EN é congruente ao lado PR e que o ângulo N é congruente ao ângulo R.

PORÉM os triângulos não são congruentes, pois Lado Lado Ângulo “LLA” não é um caso de congruência. Observe que para ser o caso Lado Ângulo Lado precisaríamos ter o ângulo entre esses dois lados, ou seja, ter o dado dos ângulos E e P.

O lado TU é congruente ao lado WX. O lado ST é congruente ao lado XV. O lado SU é congruente ao lado WV, portanto podemos afirmar que o triângulo STU é congruente ao triângulo VXW pelo caso Lado, Lado, Lado.