Exercícios de Conjuntos Numéricos - Parte IV
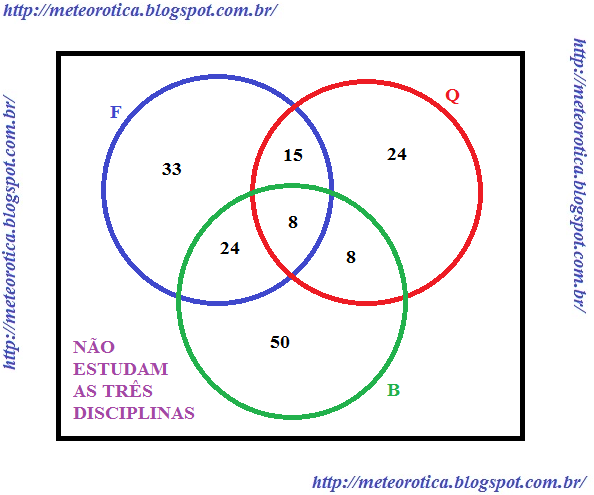
01) Numa entrevista realizada entre 200 alunos de uma faculdade constatou-se que 80 alunos estudam Física, 90, Biologia, 55, Química, 32, Biologia e Física, 23, Química e Física, 16, Biologia e Química e 8 alunos estudam as três disciplinas. Quantos alunos não estudam essas disciplinas?
Somando todos que estão em quaisquer conjuntos temos um total de 33 + 15 + 24 + 8 + 8 + 24 + 50 = 162. Como foram entrevistados 200 alunos faltam 38 que correspondem aos que não estudam as três disciplinas.
*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
02) Considere que o número de sócios de dois clubes, A e B, seja de 140. Qual é o número de sócios do clube A, se o clube B tem 60 sócios e existem 40 sócios que pertencem aos dois clubes?
Como são 140 sócios ao total, temos então que:
x + 40 + 20 = 140
x +60 =140
x = 140 - 60
x = 80
Portanto APENAS no clube A há 80 sócios, mas no clube A há no total 80 + 40 = 120 sócios, pois há os 80 que estão APENAS em A e mais os 40 que estão nos dois clubes.
*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
03) A uma reunião social compareceram 35 convidados aos quais foram oferecidos chá e café. 19 convidados tomaram chá, 4 tomaram chá e café, 7 convidados abstiveram-se de beber. Quantos convidados tomaram café?
Ao todo foram 35 convidados, então a soma de todos será 35: 15 + 4 + x + 7 = 35. Então, 26 + x = 35 -> x = 35 -26 -> x = 9. Concluímos que 9 convidados tomaram APENAS café, mas 4 tomaram chá e café, portanto também tomaram café. Assim 9 + 4 = 13 convidados tomaram café.
Ao todo foram 35 convidados, então a soma de todos será 35: 15 + 4 + x + 7 = 35. Então, 26 + x = 35 -> x = 35 -26 -> x = 9. Concluímos que 9 convidados tomaram APENAS café, mas 4 tomaram chá e café, portanto também tomaram café. Assim 9 + 4 = 13 convidados tomaram café.
*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
04) A firma produtora dos refrigerantes “Parececana” e “Parececoco” organizou uma enquete entre 2000 pessoas, e estas responderam sobre suas preferências. Sabe-se que:
800 responderam que consomem “Parececana”.
04) A firma produtora dos refrigerantes “Parececana” e “Parececoco” organizou uma enquete entre 2000 pessoas, e estas responderam sobre suas preferências. Sabe-se que:
800 responderam que consomem “Parececana”.
50 responderam que consomem os dois refrigerantes.
200 responderam que consomem “Parececoco”.
Quantas pessoas responderam que não consomem nenhum dos refrigerantes?
2000 pessoas participaram dessa enquete, então a soma de todos deverá ser:
150 + 50 + 750 + x = 2000
950 + x = 2000
x = 2000 - 950
x = 1050
Portanto, 1050 pessoas não consomem nenhum dos dois refrigerantes.
*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
05) Numa escola com seis turmas de primeiro ano de ensino médio, perfazendo um total de 160 alunos, 40 alunos reprovaram em Física, Química e Biologia. 50 reprovaram em Física e Química. 42 reprovaram em Física e Biologia. 58 reprovaram em Biologia e Química. 70 reprovaram em Física. 75 reprovaram em Química e 65 reprovaram em Biologia.
05) Numa escola com seis turmas de primeiro ano de ensino médio, perfazendo um total de 160 alunos, 40 alunos reprovaram em Física, Química e Biologia. 50 reprovaram em Física e Química. 42 reprovaram em Física e Biologia. 58 reprovaram em Biologia e Química. 70 reprovaram em Física. 75 reprovaram em Química e 65 reprovaram em Biologia.
a) Quantos alunos não reprovaram em nenhum disciplina?
RESPOSTA:
b) Quantos alunos reprovaram apenas em Física?
RESPOSTA: 18
c) Quantos alunos reprovaram apenas em Química?
RESPOSTA: 7
d) Quantos alunos reprovaram apenas em Biologia?
RESPOSTA: 5
a) RESPOSTA: como no total são 160 alunos, então os que não reprovaram nessas disciplinas estão fora dos conjuntos F, B e Q. No diagrama estão representados por "x". Assim, a soma de todos será 160:
18 + 10 + 40 +2 + 18 + 7 + 5 + x = 160
100 + x = 160
x = 160 -100
x = 60
Logo, 60 alunos não reprovaram nessas disciplinas.
*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
06) Numa cidade de 10.000 habitantes são consumidas cervejas de dois tipos A e B. Sabendo que 45% da população tomam cerveja A, 15% tomam os dois tipos de cerveja e 20% não tomam cerveja. Quantos são os habitantes que tomam da cerveja B?
06) Numa cidade de 10.000 habitantes são consumidas cervejas de dois tipos A e B. Sabendo que 45% da população tomam cerveja A, 15% tomam os dois tipos de cerveja e 20% não tomam cerveja. Quantos são os habitantes que tomam da cerveja B?
a) 3.500
b) 5.000
c) 4.000
d) 4.500
e) 1.500