Resolvi fazer uma observação dos assuntos que mais são cobrados no ENEM. Entre o conteúdo que mais aparece nas provas do ENEM na prova de Matemática podemos citar os que seguem abaixo.
Funções de 1° e 2° graus
Questões clássicas em qualquer avaliação. O aluno deve saber isolar variáveis sempre dominando as quatro operações e observando a troca de sinal dos coeficientes de uma equação quando são "passados para o outro lado". Percebendo ainda que a famosa fórmula de Bháskara pode ser calculada ou até mesmo usando soma e produto, porém na maioria das vezes é necessário analisar o valor positivo, negativo ou a igualdade do discriminante (delta).
Vamos observar uma questão do ENEM 2013 com uma ilustração de um cálice, mostrando uma representação de parábola.
Analisando a parábola representada pelo cálice vemos que a mesma "toca" o eixo "x" das abscissas, ou seja, a parábola tangencia o eixo x, mostrando que há apenas uma raiz real, assim o delta é igual a zero. Então a função f(x) = ax2 + bx + c tem seus coeficientes iguais a:
Agora vamos analisar a questão 165 do ENEM da prova amarela de 2013 segundo dia.
Porcentagem
Um dos melhores conteúdos para se trabalhar e contextualizar, além das aplicações. Vejamos a questão 163 da prova do ENEM 2013.
Questão básica sem exigência de fórmulas, mas sim interpretação, percebendo os descontos e os valores. Resolvendo teremos:
Agora vamos analisar a questão 174 da prova amarela do ENEM 2013 que envolve geometria plana e porcentagem.
Resolvendo temos:
Progressão aritmética e geométrica
Analisaremos a seguir a questão 173 do ENEM 2013. PA e PG são questões clássicas. No caso dessa questão o primeiro a perceber seria o período de 11 anos, ou seja, a cada 11 anos a atividade magnética do sol completa um ciclo. Diversas podem ser a forma de resolver, mas abaixo temos uma solução bem trabalhada em sala de aula.
Solução:
Analisaremos a seguir a questão 173 do ENEM 2013. PA e PG são questões clássicas. No caso dessa questão o primeiro a perceber seria o período de 11 anos, ou seja, a cada 11 anos a atividade magnética do sol completa um ciclo. Diversas podem ser a forma de resolver, mas abaixo temos uma solução bem trabalhada em sala de aula.
Solução:
Assim o ciclo estará na atividade magnética número 32.
Grandezas proporcionais: inversamente proporcionais ou diretamente proporcionais. Regra de três simples.
Razão e proporção. Escalas. Para exercícios resolvidos do ENEM envolvendo questões sobre escalas clique aqui.
Razão e proporção. Escalas. Para exercícios resolvidos do ENEM envolvendo questões sobre escalas clique aqui.
Equações 1º e 2º graus
Analisaremos agora uma questão que envolve intervalos aberto e fechado. Essa questão exige que o aluno crie uma equação para resolvê-la.
Como solução podemos perceber que queremos postar DUAS cartas de 100g. A massa 100g pertence ao intervalo 51g até 100g (veja que o intervalo está aberto em 50 e fechado em 100). Nessa primeira postagem será gasto então 2.1,70 = 3,40 já que esse intervalo o custo da postagem é de 1,70. Do mesmo modo para as 3 cartas de 200g teremos 3.2,65 = 7,95 (veja que o intervalo está aberto em 150g e fechado em 200g). Por fim temos mais uma postagem de 350g, então 1.4,00 = 4,00 (veja que o intervalo está aberto em 300 e fechado em 350g). Portanto será gasto:
3,40 + 7,95 + 4,00 = 15,35.
Analisaremos agora uma questão que envolve intervalos aberto e fechado. Essa questão exige que o aluno crie uma equação para resolvê-la.
Como solução podemos perceber que queremos postar DUAS cartas de 100g. A massa 100g pertence ao intervalo 51g até 100g (veja que o intervalo está aberto em 50 e fechado em 100). Nessa primeira postagem será gasto então 2.1,70 = 3,40 já que esse intervalo o custo da postagem é de 1,70. Do mesmo modo para as 3 cartas de 200g teremos 3.2,65 = 7,95 (veja que o intervalo está aberto em 150g e fechado em 200g). Por fim temos mais uma postagem de 350g, então 1.4,00 = 4,00 (veja que o intervalo está aberto em 300 e fechado em 350g). Portanto será gasto:
3,40 + 7,95 + 4,00 = 15,35.
Trigonometria (triângulo retângulo e semelhança de triângulos)
Para saber mais sobre semelhança de triângulos clique aqui
Analisando a questão 179 de matemática do ENEM 2013 temos uma clássica questão de trigonometria e sua semelhança de triângulos. Veja a questão abaixo e, em seguida, a resolução:
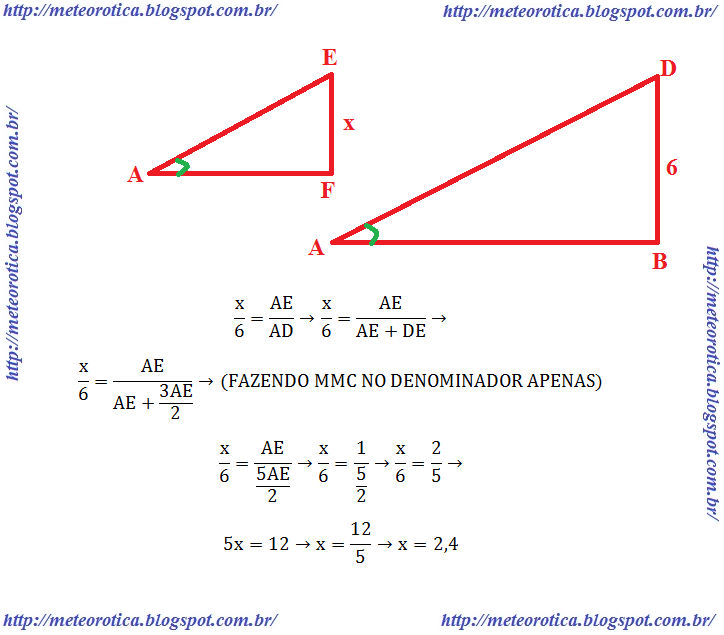
Perceba que o ponto E define dois ângulos opostos pelo vértice. Primeiro nomine esses dois ângulos de "alfa". Em seguida perceba que os triângulo ACE é semelhante ao triângulo DBE, então nomine o ângulo A e o ângulo D como "beta". Olhe para a figura abaixo:
Após essa comparação podemos fazer outra com os triângulos ACE e ABD. Perceba que o lado oposto ao ângulo em A é "x" no triângulo ACE e é 6 no triângulo ABD. Assim podemos escrever "x está para 6 assim como a medida AE está para a medida AD", onde AD é a medida AE mais a medida DE que já obtivemos acima.
Para saber mais sobre semelhança de triângulos clique aqui
Analisando a questão 179 de matemática do ENEM 2013 temos uma clássica questão de trigonometria e sua semelhança de triângulos. Veja a questão abaixo e, em seguida, a resolução:
Perceba que o ponto E define dois ângulos opostos pelo vértice. Primeiro nomine esses dois ângulos de "alfa". Em seguida perceba que os triângulo ACE é semelhante ao triângulo DBE, então nomine o ângulo A e o ângulo D como "beta". Olhe para a figura abaixo:
Após essa comparação podemos fazer outra com os triângulos ACE e ABD. Perceba que o lado oposto ao ângulo em A é "x" no triângulo ACE e é 6 no triângulo ABD. Assim podemos escrever "x está para 6 assim como a medida AE está para a medida AD", onde AD é a medida AE mais a medida DE que já obtivemos acima.
Áreas de figuras planas/prismas, cilindros, cones e esferas - Geometria Espacial no ENEM clique aqui
Análise combinatória e probabilidade
Para mais questões do ENEM sobre combinatória e probabilidade clique aqui
Na próxima questão também da prova do ENEM 2013. As informações da questão fornece um número de compradores para cada produto em cada mês. Note o total de compradores do produto A é 100 (10 no mês de janeiro, 30 no mês de fevereiro e 60 no mês de março), já os compradores do produto B são 120 (20 no mês de janeiro, 20 no mês de fevereiro e 80 no mês de março). Vamos calcular a probabilidade do sorteado no mês de fevereiro para os produtos A e B:
Resolvendo:
Para mais questões do ENEM sobre combinatória e probabilidade clique aqui
Na próxima questão também da prova do ENEM 2013. As informações da questão fornece um número de compradores para cada produto em cada mês. Note o total de compradores do produto A é 100 (10 no mês de janeiro, 30 no mês de fevereiro e 60 no mês de março), já os compradores do produto B são 120 (20 no mês de janeiro, 20 no mês de fevereiro e 80 no mês de março). Vamos calcular a probabilidade do sorteado no mês de fevereiro para os produtos A e B:
Resolvendo:
Agora vamos analisar a questão 165 da prova Azul ou 157 da prova Branca ou 171 da prova Rosa ou 161 da prova Amarela. Muitos queriam anular a questão devido ao gabarito inadequado, mas vamos resolvê-la antes de falar sobre isso:
Solução: em A podemos colocar 3 cores, feito isso para B sobram duas e para D também sobram duas (D e B podem ser iguais, mas diferentes de A). Colocando 3 em A, duas possibilidades em B e D e em C mais duas possibilidades. Logo temos 3.2.2.2= 24. Como os elementos se repetem (A e C mesma cor e B e D mesma cor) temos uma combinação com elementos repetidos, portanto o resultado fica dividido por 2, assim teremos 24/2 = 12 joias diferentes. (letra B)
O enunciado não considerou a repetição de cores não consecutivas sem falar que temos de considerar que não importa se essas cores repetidas trocarem de lugar entre si, é uma combinação com elementos repetidos.
Com relação ao gabarito, está correto e não inadequado como muito pensaram nos casos em que as pedras em D e B fossem iguais e contariam mais uma opção de joia o mesmo iguais em A e C.
Ou ainda pense: há 3 cores e 4 posições, uma das cores terá que se repetir. Como os vértices consecutivos devem ter cores distintas a repetição só ocorrerá entre A e C ou B e D.
Considerando A e C iguais, para cada cor de A e C há duas outras para B e D. Logo, temos 3 × 2 = 6 possibilidades.
Quando B e D são distintos, temos 3 possibilidades de organizar as cores.
Por último temos os casos em que A e C são diferentes (são mais 3 possibilidades, uma para cada cor em B e D). Portanto, 3 + 6 + 3 = 12 possibilidades.
Nenhum comentário:
Postar um comentário